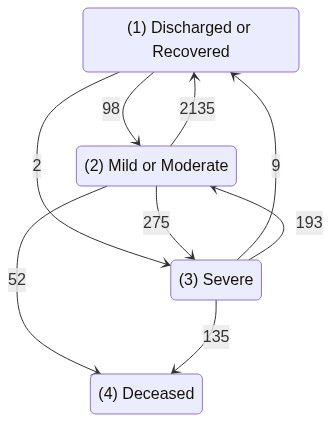
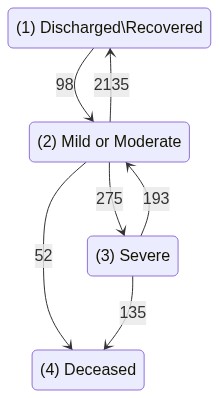
COVID hospitalization example
In this notebook¤
This notebook provides an example of using the pymsm package in a more complex setting which includes recurring events and time-varying covariates.
We will also see how to load a saved model and run simualtions.
For all this, we will use Israel COVID-19 hospitalization public data, as described in Roimi et. al. 2021.
# Imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pymsm.datasets import prep_covid_hosp_data
from pymsm.multi_state_competing_risks_model import MultiStateModel
from pymsm.statistics import (
prob_visited_states,
stats_total_time_at_states,
get_path_frequencies,
path_total_time_at_states
)
from pymsm.simulation import MultiStateSimulator
%load_ext autoreload
%autoreload 2
Load data¤
Let's look at one patients path
For the example above, we see a man aged 72.5,
who follows a path of "Mild or Moderate"->"Severe"->"Deceased"
with transition times of 6 and 31 days.
Path frequencies¤
We can print out a summary for all different trajectories in the data
Define time-varying covariates¤
We can define a custom "update_covariates_function" such as below:
def covid_update_covariates_function(
covariates_entering_origin_state,
origin_state=None,
target_state=None,
time_at_origin=None,
abs_time_entry_to_target_state=None,
):
covariates = covariates_entering_origin_state.copy()
# update is_severe covariate
if origin_state == 3:
covariates['was_severe'] = 1
# # update cum_hosp_tim covariate
# if ((origin_state==2) & (origin_state==3)):
# covariates["cum_hosp_time"] += time_at_origin
return covariates
Fitting the Multistate model¤
Note that we get some warnings for some of the transitions. These should be handled or at least acknowledged when fitting a model.
Another option might be to discard these transitions that contain a small number of samples. We can set the trim_transitions_threshold to a minimal nuber of samples for which a model will be trained.
Let's set this to 10 below
Trimming transitions¤
Single patient stats¤
Let's take a look at how the model models transitions for a single patient - a female aged 75
We'll run a Monte-Carlo simulation for 100 samples and present some path statistics
Let's calculate the probability of being in any of the states and also obtain stats regarding time in each state
# Probability of visiting any of the states
for state, state_label in state_labels.items():
if state == 0:
continue
print(
f"Probabilty of ever being {state_label} = {prob_visited_states(mc_paths, states=[state])}"
)
# Stats for times at states
dfs = []
for state, state_label in state_labels.items():
if state == 0 or state in terminal_states:
continue
dfs.append(
pd.DataFrame(
data=stats_total_time_at_states(mc_paths, states=[state]),
index=[state_label],
)
)
pd.concat(dfs).round(3).T
Print out the path frequencies for the sampled paths
A CDF for the total time in hospital
We can also look at Monte-Carlo simulations for the same patient, assuming we already know she has been in the Severe (3) state, for 2 days.
To do this, we simply need to set the origin_state to 3, set the current_time to 2, and update her covariates accordingly.
Now we can calculate the probability of being in any of the states and obtain statistics regarding time in each state.
We can compare these to the statistics we obtained above, when the patient started in a Mild (2) state.
# Probability of visiting any of the states
for state, state_label in state_labels.items():
if state == 0:
continue
print(
f"Probabilty of ever being {state_label} = {prob_visited_states(mc_paths_severe, states=[state])}"
)
# Stats for times at states
dfs = []
for state, state_label in state_labels.items():
if state == 0 or state in terminal_states:
continue
dfs.append(
pd.DataFrame(
data=stats_total_time_at_states(mc_paths_severe, states=[state]),
index=[state_label],
)
)
pd.concat(dfs).round(3).T
Saving the model and configuring a simulator¤
We can save the model for later use, and configure a simulator to generate simulated paths
from pymsm.simulation import extract_competing_risks_models_list_from_msm
competing_risks_models_list = extract_competing_risks_models_list_from_msm(
multi_state_model, verbose=True
)
# Configure the simulator
mssim = MultiStateSimulator(
competing_risks_models_list,
terminal_states=[5, 6],
update_covariates_fn=covid_update_covariates_function,
covariate_names=covariate_cols,
state_labels=state_labels,
)
And now we can sample paths from this simulator