Skip to content

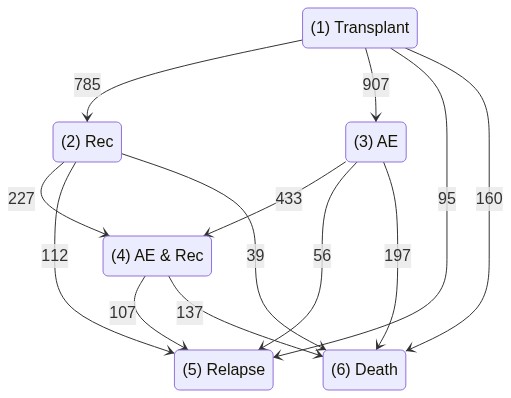
The EBMT dataset¤

import pandas as pd
from pymsm.multi_state_competing_risks_model import  MultiStateModel

Data from the European Society for Blood and Marrow Transplantation (EBMT)

A data frame of 2279 patients transplanted at the EBMT between 1985 and 1998.
(from R mstate package, see: https://www.rdocumentation.org/packages/mstate/versions/0.3.1/topics/EBMT%20data) 

from pymsm.datasets import load_ebmt, prep_ebmt_long, plot_ebmt
load_ebmt().head()
id from to trans Tstart Tstop time status match proph year agecl
1 1 1 2 1 0.0 22.0 22.0 1 no gender mismatch no 1995-1998 20-40
2 1 1 3 2 0.0 22.0 22.0 0 no gender mismatch no 1995-1998 20-40
3 1 1 5 3 0.0 22.0 22.0 0 no gender mismatch no 1995-1998 20-40
4 1 1 6 4 0.0 22.0 22.0 0 no gender mismatch no 1995-1998 20-40
5 1 2 4 5 22.0 995.0 973.0 0 no gender mismatch no 1995-1998 20-40 
competing_risk_dataset, covariate_cols, state_labels = prep_ebmt_long()
competing_risk_dataset.head()
sample_id origin_state target_state time_entry_to_origin time_transition_to_target match_no gender mismatch proph_yes year_1990-1994 year_1995-1998 agecl_<=20 agecl_>40
0 1 1 2 0.0 22.0 1 0 0 1 0 0
1 1 2 0 22.0 995.0 1 0 0 1 0 0
2 2 1 3 0.0 12.0 1 0 0 1 0 0
3 2 3 4 12.0 29.0 1 0 0 1 0 0
4 2 4 5 29.0 422.0 1 0 0 1 0 0 
plot_ebmt(competing_risk_dataset, state_labels, covariate_cols, terminal_states=[5, 6])

Multi-state model based on Survival-Trees¤

terminal_states = [5, 6]

multi_state_model = MultiStateModel(
    dataset=competing_risk_dataset,
    terminal_states=terminal_states,
    covariate_names=covariate_cols,
    competing_risk_data_format=True,
    state_labels=state_labels
)


multi_state_model.fit()

Fitting Model at State: 1
>>> Fitting Transition to State: 2, n events: 785
>>> Fitting Transition to State: 3, n events: 907
>>> Fitting Transition to State: 5, n events: 95
>>> Fitting Transition to State: 6, n events: 160
Fitting Model at State: 2
>>> Fitting Transition to State: 5, n events: 112
>>> Fitting Transition to State: 6, n events: 39
>>> Fitting Transition to State: 4, n events: 227
Fitting Model at State: 3
>>> Fitting Transition to State: 4, n events: 433
>>> Fitting Transition to State: 6, n events: 197
>>> Fitting Transition to State: 5, n events: 56
Fitting Model at State: 4
>>> Fitting Transition to State: 5, n events: 107
>>> Fitting Transition to State: 6, n events: 137

Single patient statistics¤

# Run MC for a sample single patient
mc_paths = multi_state_model.run_monte_carlo_simulation(
    sample_covariates=competing_risk_dataset.loc[0, covariate_cols],
    origin_state=1,
    current_time=0,
    n_random_samples=1000,
    max_transitions=10,
)

 20%|██        | 200/1000 [00:34<02:02,  6.53it/s]/workspaces/pymsm/src/pymsm/multi_state_competing_risks_model.py:600: RuntimeWarning: invalid value encountered in true_divide
  probability_for_each_t / probability_for_each_t.max()
 66%|██████▋   | 664/1000 [01:41<00:48,  7.00it/s]/workspaces/pymsm/src/pymsm/multi_state_competing_risks_model.py:600: RuntimeWarning: invalid value encountered in true_divide
  probability_for_each_t / probability_for_each_t.max()
 79%|███████▉  | 792/1000 [01:59<00:30,  6.82it/s]/workspaces/pymsm/src/pymsm/multi_state_competing_risks_model.py:600: RuntimeWarning: invalid value encountered in true_divide
  probability_for_each_t / probability_for_each_t.max()
100%|█████████▉| 996/1000 [02:29<00:00,  6.93it/s]/workspaces/pymsm/src/pymsm/multi_state_competing_risks_model.py:600: RuntimeWarning: invalid value encountered in true_divide
  probability_for_each_t / probability_for_each_t.max()
100%|██████████| 1000/1000 [02:29<00:00,  6.68it/s]


from pymsm.statistics import prob_visited_states, stats_total_time_at_states

all_states = competing_risk_dataset["target_state"].unique()
# Probability of visiting any of the states
for state in all_states:
    if state == 0:
        continue
    print(
        f"Probabilty of {state_labels[state]} = {prob_visited_states(mc_paths, states=[state])}"
    )

# Probability of terminal states - Death and Relapse
print(
    f"Probabilty of any terminal state = {prob_visited_states(mc_paths, states=multi_state_model.terminal_states)}"
)

Probabilty of Rec = 0.521
Probabilty of AE = 0.37
Probabilty of AE & Rec = 0.677
Probabilty of Relapse = 0.305
Probabilty of Death = 0.695
Probabilty of any terminal state = 1.0


# Stats for times at states
dfs = []
for state in all_states:
    if state == 0 or state in terminal_states:
        continue
    dfs.append(
        pd.DataFrame(
            data=stats_total_time_at_states(mc_paths, states=[state]),
            index=[state_labels[state]],
        )
    )
pd.concat(dfs)
time_in_state_mean time_in_state_std time_in_state_median time_in_state_min time_in_state_max time_in_state_quantile_0.1 time_in_state_quantile_0.25 time_in_state_quantile_0.75 time_in_state_quantile_0.9
Rec 71.842996 382.733580 0.999979 0.0 4228.999967 0.0 0.0 18.000004 56.099967
AE 76.118467 380.102104 0.000000 0.0 4702.999975 0.0 0.0 15.999921 105.999959
AE & Rec 1020.443978 1607.097318 137.999967 0.0 4761.999903 0.0 0.0 1150.499969 4205.999946